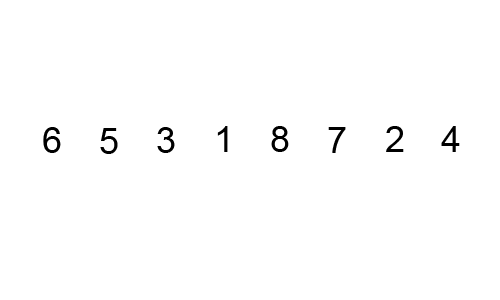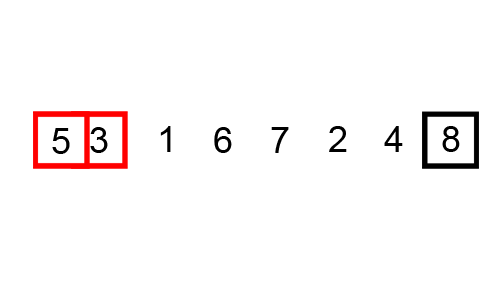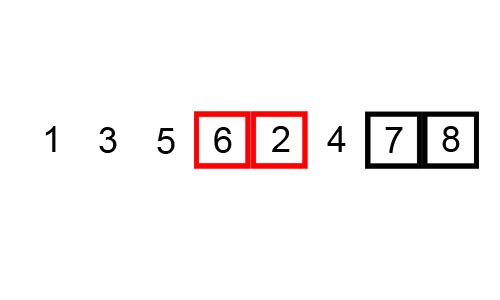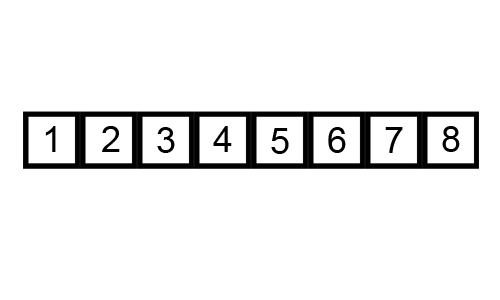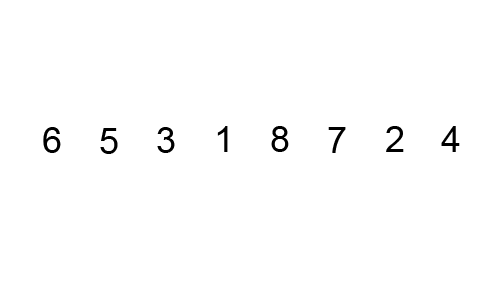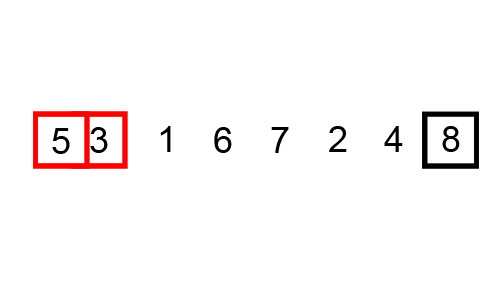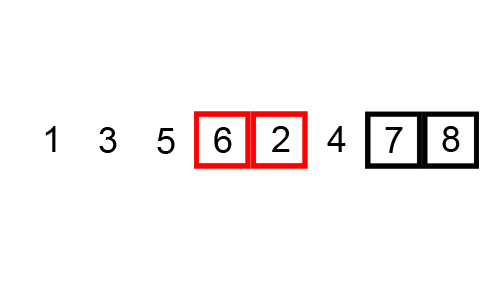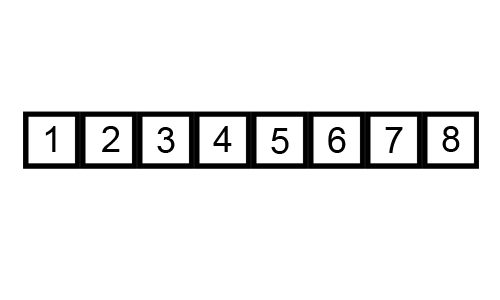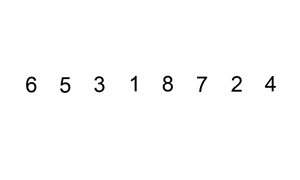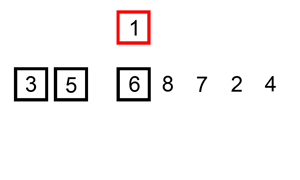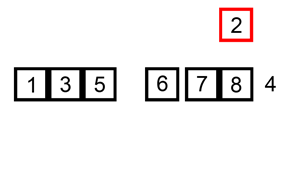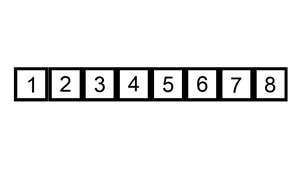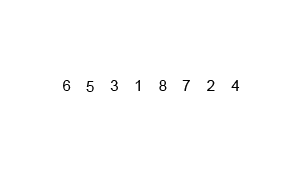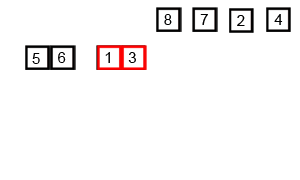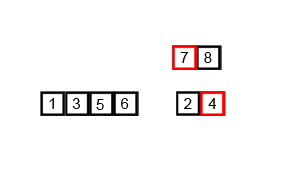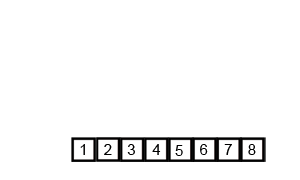정렬 알고리즘
1. 선택 정렬 (Selection Sort)
前から順番に整列する方法である。まず、与えられたリストの中で最小値を求めて、その値を一番前の数値と入れ替える方式
앞에서부터 차례대로 정렬하는 방법이다. 먼저 주어진 리스트중 최소값을 구하고, 그 값을 맨 앞의 값과 교체하는 방식
最適効率は下順に整列されているデータを上順に整列する時であり、逆に既に整列されている状態で少数のデータが追加になって再整列する時に最悪の整列処理速度になる。
최적 효율은 내림차순으로 정렬되어 있는 데이터를 오름차순으로 정렬할 때이며, 반대로 이미 정렬된 상태에서 소수 데이터가 추가됨으로 재정렬하게 될 때에는 최악의 처리 속도를 보여준다.
2. 버블정렬 (Bubble Sort)
最初のものから隣接したものを比較して交換しながら最後まで整列する方式である。
첫 번째 원소부터 인접한 원소끼리 계속 자리를 교환하면서 맨 끝부터 정렬하는 방식을 말한다.
データを一つずつ比較することができて精密に比較できるが、比較回数が多くなるので性能的に良い方法ではない。
데이터를 하나씩 비교할 수 있어 정밀하게 비교 가능하나 비교횟수가 많아지므로 성능면에서 좋은 방법이 아니다.
3. 삽입정렬 (Insertion Sort)
配列の全てのものを前から順番に既に整列された配列部分と比べて自分の位置を探して挿入して整列を完成する整列方法である。
배열의 모든 요소를 앞에서부터 차례대로 이미 정렬된 배열 부분과 비교하여 자신의 위치를 찾아 삽입함으로써 정렬을 완성하는 정렬 방법이다.
バブル整列を比較回数を減らしてより良い性能効率を出せる。
버블정렬의 비교횟수를 줄이고 보다 좋은 성능 효율을 보여준다.
4. 합병정렬 (Merge Sort)
小さい単位で分けて小さい単位から整列して整列された単位をずっと併合していく整列方式である。
작은 단위로 잘게 쪼개어 작은 단위부터 정렬해서 정렬된 단위들을 계속 병합해가는 정렬 방식이다.
簡単でし易く安全性があり、良い性能を見せる。空間が多く必要という短所がある。
간단하고 쉽고 안정성이 있어 좋은 성능을 보여준다. 공간이 많이 필요하다는 단점이 있다.
5. 퀵 정렬 (Quick Sort)
連続的な分割による整列方式である。最初は築を決めて築より小さい方は左に、大きい方は右に位置して左と右の数字はまたそれぞれの築に分けて築の値が1になるまで整列する。
연속적인 분할에 의한 정렬 방식이다. 처음 하나의 축(Pivot)을 정하여 이 축의 값보다 작은 값은 왼쪽에 큰 값은 오른쪽으로 위치시킨뒤 왼쪽과 오른쪽의 수 들은 다시 각각의 축으로 나누어져 축값이 1이 될 때까지 정렬한다.
一番多く使用されるが安全性が落ちるという短所がある。
가장 많이 사용되나 안정성이 떨어진다는 단점이 있다.
6. 힙 정렬 (Heap Sort)
最大 Hip tree や 最小 Hip tree を構成して整列する方法である。全てのノードが Hip 属性(各ノードの値が自分の子ノードの値より大きい2進トリー)を満足する様に再帰的に Tree構造を作って整列を完成する。
최대 힙 트리나 최소 힙 트리를 구성해 정렬하는 방법이다. 모든 노드가 힙 속성(각 노드의 값이 자신의 자식노드 값보다 큰 이진트리)을 만족하도록 재귀적으로 트리 구조를 만들어 정렬을 완성한다.
付加的なメモリーが全く必要ないというのが大きな長所だ。
부가적인 메모리가 전혀 필요없다는 게 큰 장점이다.
7. 쉘 정렬(Shell Sort)
삽입 정렬을 보완한 알고리즘이다. 쉘 정렬은 정렬해야 할 리스트를 일정한 간격에 따라 나눈다. 그렇게 여러개로 나누어진 부분 리스트를 만들어 각 부분 리스트를 삽입 정렬을 이용해 정렬하는 방식이다.
8. 기수 정렬(Radix Sort)
주어진 수들간의 비교를 하지않고 버킷을 사용해 정렬하는 방법. 낮은 자리(1의 자리)에서 높은 자리(10^n 자리) 순으로 버킷에 넣는 방법으로 정렬한다.
실제로 숫자들 간의 비교를 통해 정렬을 하는 것이 아닌, 0~9까지의 버킷이 있고 이 버킷에 숫자를 넣어가며 분류한다고 생각하면 된다.
시간 복잡도에서 엄청난 이점을 가지지만 추가적인 메모리가 매우 필요하다.
9. 정렬 알고리즘 예상질문
1. Quick sort가 항상 빠르고 좋은가?
정렬하고자 하는 데이터의 크기 n이 작을때를 가정해보자. 계속해서 재귀적으로 partition 함수를 호출하는 퀵 정렬로만 정렬한다면 n이 작을 때 함수를 호출하는 비용이 더 많이 들것이다. 즉, n이 작아진 경우에는 다른 정렬 알고리즘을 통해 정렬하는 것이 더 효율적일 수 있다. n값이 작을 때, nlongn 과 n^2 차이는 미미하므로 삽입 정렬로 구현하는 것이 더 효율적일 수 있다. 실제로 Java에서 퀵 정렬의 구현이 이렇게 되어있다. n값이 작을 때는 삽입 정렬로 정렬한다.
2. Merge sort는 언제 쓰일까?
한정된 메모리 상황에서 빅 데이터를 정렬해야 하는 경우를 가정하자. 기존의 정렬 알고리즘으로 한번에 정렬 할 수 없는.. 디스크에서 읽어오는데 데이터 전부를 메모리에 올리지 못하는 경우 말이다. 그래서 이 큰 문제를 작은 문제로 나누어 정렬한다. 작은 문제로 나누어진 데이터를 퀵 정렬로 정렬한 뒤 각각 정렬된 데이터들을 다시 합쳐야한다. 하지만 그냥 합친다면 작은 문제로 정렬한 의미가 없어지므로 이 경우에 merge sort 를 사용하여 합치는 것이다. 즉, Merge sort는 DB에 많이 쓰인다.
1. 선택 정렬 (Selection Sort)
前から順番に整列する方法である。まず、与えられたリストの中で最小値を求めて、その値を一番前の数値と入れ替える方式
앞에서부터 차례대로 정렬하는 방법이다. 먼저 주어진 리스트중 최소값을 구하고, 그 값을 맨 앞의 값과 교체하는 방식
最適効率は下順に整列されているデータを上順に整列する時であり、逆に既に整列されている状態で少数のデータが追加になって再整列する時に最悪の整列処理速度になる。
최적 효율은 내림차순으로 정렬되어 있는 데이터를 오름차순으로 정렬할 때이며, 반대로 이미 정렬된 상태에서 소수 데이터가 추가됨으로 재정렬하게 될 때에는 최악의 처리 속도를 보여준다.
2. 버블정렬 (Bubble Sort)
最初のものから隣接したものを比較して交換しながら最後まで整列する方式である。
첫 번째 원소부터 인접한 원소끼리 계속 자리를 교환하면서 맨 끝부터 정렬하는 방식을 말한다.
データを一つずつ比較することができて精密に比較できるが、比較回数が多くなるので性能的に良い方法ではない。
데이터를 하나씩 비교할 수 있어 정밀하게 비교 가능하나 비교횟수가 많아지므로 성능면에서 좋은 방법이 아니다.
3. 삽입정렬 (Insertion Sort)
配列の全てのものを前から順番に既に整列された配列部分と比べて自分の位置を探して挿入して整列を完成する整列方法である。
배열의 모든 요소를 앞에서부터 차례대로 이미 정렬된 배열 부분과 비교하여 자신의 위치를 찾아 삽입함으로써 정렬을 완성하는 정렬 방법이다.
バブル整列を比較回数を減らしてより良い性能効率を出せる。
버블정렬의 비교횟수를 줄이고 보다 좋은 성능 효율을 보여준다.
4. 합병정렬 (Merge Sort)
小さい単位で分けて小さい単位から整列して整列された単位をずっと併合していく整列方式である。
작은 단위로 잘게 쪼개어 작은 단위부터 정렬해서 정렬된 단위들을 계속 병합해가는 정렬 방식이다.
簡単でし易く安全性があり、良い性能を見せる。空間が多く必要という短所がある。
간단하고 쉽고 안정성이 있어 좋은 성능을 보여준다. 공간이 많이 필요하다는 단점이 있다.
5. 퀵 정렬 (Quick Sort)
連続的な分割による整列方式である。最初は築を決めて築より小さい方は左に、大きい方は右に位置して左と右の数字はまたそれぞれの築に分けて築の値が1になるまで整列する。
연속적인 분할에 의한 정렬 방식이다. 처음 하나의 축(Pivot)을 정하여 이 축의 값보다 작은 값은 왼쪽에 큰 값은 오른쪽으로 위치시킨뒤 왼쪽과 오른쪽의 수 들은 다시 각각의 축으로 나누어져 축값이 1이 될 때까지 정렬한다.
一番多く使用されるが安全性が落ちるという短所がある。
가장 많이 사용되나 안정성이 떨어진다는 단점이 있다.
6. 힙 정렬 (Heap Sort)
最大 Hip tree や 最小 Hip tree を構成して整列する方法である。全てのノードが Hip 属性(各ノードの値が自分の子ノードの値より大きい2進トリー)を満足する様に再帰的に Tree構造を作って整列を完成する。
최대 힙 트리나 최소 힙 트리를 구성해 정렬하는 방법이다. 모든 노드가 힙 속성(각 노드의 값이 자신의 자식노드 값보다 큰 이진트리)을 만족하도록 재귀적으로 트리 구조를 만들어 정렬을 완성한다.
付加的なメモリーが全く必要ないというのが大きな長所だ。
부가적인 메모리가 전혀 필요없다는 게 큰 장점이다.
7. 쉘 정렬(Shell Sort)
삽입 정렬을 보완한 알고리즘이다. 쉘 정렬은 정렬해야 할 리스트를 일정한 간격에 따라 나눈다. 그렇게 여러개로 나누어진 부분 리스트를 만들어 각 부분 리스트를 삽입 정렬을 이용해 정렬하는 방식이다.
8. 기수 정렬(Radix Sort)
주어진 수들간의 비교를 하지않고 버킷을 사용해 정렬하는 방법. 낮은 자리(1의 자리)에서 높은 자리(10^n 자리) 순으로 버킷에 넣는 방법으로 정렬한다.
실제로 숫자들 간의 비교를 통해 정렬을 하는 것이 아닌, 0~9까지의 버킷이 있고 이 버킷에 숫자를 넣어가며 분류한다고 생각하면 된다.
시간 복잡도에서 엄청난 이점을 가지지만 추가적인 메모리가 매우 필요하다.
9. 정렬 알고리즘 예상질문
1. Quick sort가 항상 빠르고 좋은가?
정렬하고자 하는 데이터의 크기 n이 작을때를 가정해보자. 계속해서 재귀적으로 partition 함수를 호출하는 퀵 정렬로만 정렬한다면 n이 작을 때 함수를 호출하는 비용이 더 많이 들것이다. 즉, n이 작아진 경우에는 다른 정렬 알고리즘을 통해 정렬하는 것이 더 효율적일 수 있다. n값이 작을 때, nlongn 과 n^2 차이는 미미하므로 삽입 정렬로 구현하는 것이 더 효율적일 수 있다. 실제로 Java에서 퀵 정렬의 구현이 이렇게 되어있다. n값이 작을 때는 삽입 정렬로 정렬한다.
2. Merge sort는 언제 쓰일까?
한정된 메모리 상황에서 빅 데이터를 정렬해야 하는 경우를 가정하자. 기존의 정렬 알고리즘으로 한번에 정렬 할 수 없는.. 디스크에서 읽어오는데 데이터 전부를 메모리에 올리지 못하는 경우 말이다. 그래서 이 큰 문제를 작은 문제로 나누어 정렬한다. 작은 문제로 나누어진 데이터를 퀵 정렬로 정렬한 뒤 각각 정렬된 데이터들을 다시 합쳐야한다. 하지만 그냥 합친다면 작은 문제로 정렬한 의미가 없어지므로 이 경우에 merge sort 를 사용하여 합치는 것이다. 즉, Merge sort는 DB에 많이 쓰인다.